揭秘:解释变量与自变量,被解释变量与因变量的真实关系!
在统计学与数据分析的广阔领域中,我们经常会遇到各种各样的术语,其中“解释变量”与“被解释变量”,“自变量”与“因变量”是几组尤为重要的概念。这些术语虽然在表面上看似相似,但实际上在定义、作用以及应用上有着细微却至关重要的差别。本文旨在深入探讨“解释变量就是自变量吗?”以及“被解释变量就是因变量吗?”这两个问题,以期帮助读者在数据分析的道路上更加游刃有余。
首先,让我们从基础概念出发。自变量,又称独立变量,是指在实验中能够主动改变或选择的变量,它的变化不受其他变量的影响,而是可以独立地取值。在统计学模型中,自变量通常被用来预测或解释其他变量的变化。例如,在研究一个地区的气温与冰淇淋销量的关系时,气温就是一个典型的自变量,因为我们可以观察到气温的变化,并且这种变化是独立于冰淇淋销量的。

而因变量,又称依赖变量,是指在实验中随自变量变化而变化的变量。它的取值依赖于自变量的取值,因此被称为“因”于自变量。在上述冰淇淋销量的例子中,销量就是一个因变量,因为它会随着气温的变化而变化。简而言之,自变量是“因”的发起者,而因变量是“果”的接受者。
接下来,我们转向解释变量与被解释变量的概念。在回归分析等统计模型中,解释变量是指那些被用来解释或预测另一个变量(被解释变量)的变量。从某种程度上说,解释变量在模型中扮演着“原因”的角色,它们通过某种方式影响着被解释变量的取值。在回归分析中,解释变量通常与自变量是同义词,因为它们都是用来预测或解释其他变量的。然而,需要注意的是,这种等同并不是绝对的,特别是在复杂的统计模型中,解释变量的概念可能会更加宽泛,它可能不仅仅包括自变量,还可能包括一些用于调整模型精度的其他变量。
被解释变量,又称响应变量或预测目标,是模型中我们希望用解释变量来预测或解释的变量。在回归分析中,被解释变量通常与因变量是同义词,因为它们都是模型中“被影响”的变量。被解释变量的取值是模型预测或解释的重点,也是数据分析师最关心的结果之一。
现在,我们回到文章开头的问题:“解释变量就是自变量吗?被解释变量就是因变量吗?”在大多数情况下,特别是在简单的回归分析中,这两组术语是可以互换使用的。解释变量在模型中扮演着与自变量相同的角色——它们是用来预测或解释被解释变量(或因变量)的。同样,被解释变量在模型中也与因变量相对应,都是模型中需要预测或解释的目标。
然而,我们也需要认识到,这种等同并不是在所有情况下都成立。特别是在复杂的统计模型中,解释变量的概念可能会更加宽泛和灵活。例如,在多元回归分析中,解释变量可能包括多个自变量以及它们之间的交互项、平方项等非线性项。此外,在某些情况下,被解释变量可能不仅仅是一个单一的因变量,而是由多个变量组成的向量或矩阵。因此,虽然解释变量与被解释变量在概念上与自变量和因变量有很大的重叠,但在具体应用中,我们仍然需要根据模型的复杂性和数据的特性来准确理解这些术语的含义。
此外,还需要注意的是,解释变量与被解释变量(以及自变量与因变量)之间的关系并不是单向的。在一个模型中,一个变量可能是解释变量(或自变量),但在另一个模型中,它可能变成被解释变量(或因变量)。这种灵活性是数据分析中常见的一个特点,它允许我们根据不同的研究目的和数据特性来构建不同的模型。
综上所述,解释变量在大多数情况下可以等同于自变量,被解释变量也可以等同于因变量。这种等同在简单的回归分析中尤为明显。然而,在复杂的统计模型中,我们仍然需要谨慎地理解这些术语的含义和区别。通过深入理解这些概念以及它们在模型中的作用,我们可以更加准确地构建和分析统计模型,从而为数据驱动的决策提供更加有力的支持。
在数据分析的实践中,准确理解并应用这些术语是至关重要的。它们不仅是我们构建模型的基础,也是我们解读模型结果、提取有价值信息的关键。因此,无论是在学术研究还是商业分析中,我们都应该认真对待这些概念的学习和应用,以确保我们的分析过程既准确又高效。
最后,需要强调的是,数据分析是一个不断发展和变化的领域。随着新的统计方法和计算技术的不断涌现,我们对这些术语的理解和应用也可能会随之变化。因此,保持对最新研究成果和实践经验的关注和学习是我们作为数据分析师的重要责任之一。只有这样,我们才能不断提升自己的专业能力,为数据驱动的未来做出更大的贡献。
-
 揭秘:轻松区分因变量与自变量,让你的数据分析更上一层楼!资讯攻略10-31
揭秘:轻松区分因变量与自变量,让你的数据分析更上一层楼!资讯攻略10-31 -
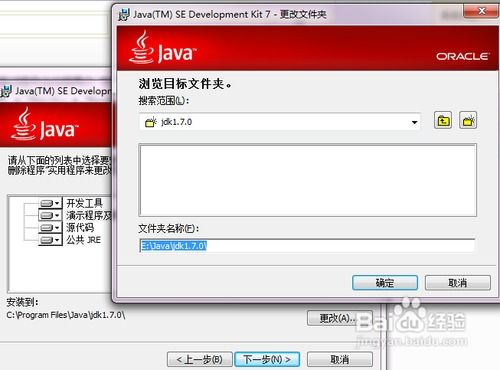 如何配置JDK的环境变量?资讯攻略11-21
如何配置JDK的环境变量?资讯攻略11-21 -
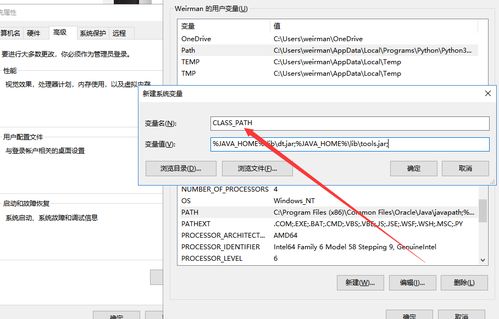 怎样正确配置Java环境变量?资讯攻略11-04
怎样正确配置Java环境变量?资讯攻略11-04 -
 深入解析Jensen不等式资讯攻略01-11
深入解析Jensen不等式资讯攻略01-11 -
 轻松学会制作曲线图的方法资讯攻略10-30
轻松学会制作曲线图的方法资讯攻略10-30 -
 CPK计算公式及其详细解释是什么?资讯攻略11-14
CPK计算公式及其详细解释是什么?资讯攻略11-14












