轻松学会:两点间斜率求解方法
探索直线斜率:从两点出发的奇妙之旅
在数学的世界里,直线是最简单而又充满魅力的图形之一。它笔直无曲,连接着两个点,似乎在无声地诉说着“最短的距离即是直线”的真理。而在直线的众多属性中,斜率(slope)无疑是最为引人关注的一个。斜率不仅描述了直线的倾斜程度,更在解析几何、微积分等多个数学领域中发挥着重要作用。今天,就让我们一同踏上一段从两点出发的奇妙旅程,探索如何求解直线的斜率,感受数学之美。

一、初识斜率:直线倾斜的量化
想象一下,你站在一片广袤的草原上,远处有两座山峰,它们在你的视线中构成了一条直线。这条直线的倾斜程度,或平缓如微风拂过水面,或陡峭似悬崖峭壁,我们如何量化这种倾斜呢?答案就是斜率。

斜率,用数学符号表示为“m”,它描述了直线上升或下降的“快慢”。具体来说,斜率等于直线上任意两点间纵坐标差与横坐标差之商。这个定义听起来有些抽象,但当我们实际操作时,就会发现它其实非常直观。

二、两点确定斜率:一个简单的公式
要计算直线的斜率,我们至少需要知道直线上的两个点。这两个点就像是直线的“坐标锚”,它们的位置决定了直线的方向和倾斜程度。
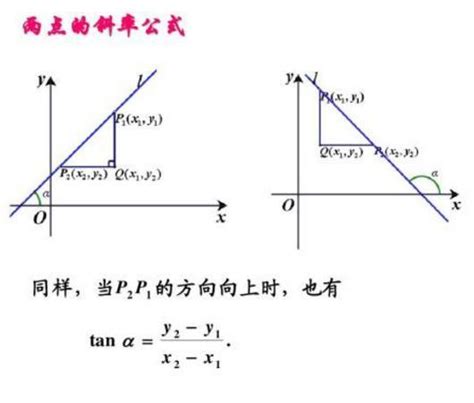
假设我们有两个点A(x₁, y₁)和B(x₂, y₂),那么直线AB的斜率m可以通过以下公式计算得出:
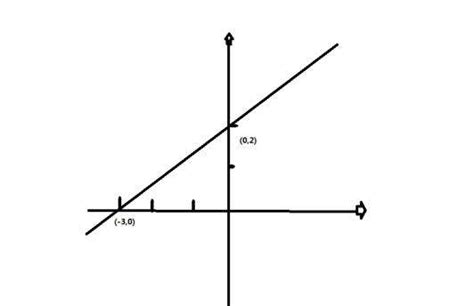
m = (y₂ - y₁) / (x₂ - x₁)
这个公式看似简单,却蕴含着深刻的数学原理。它告诉我们,斜率实际上是纵坐标变化量与横坐标变化量的比值,这个比值反映了直线在不同方向上的“坡度”。
三、理解斜率公式的内涵
在斜率公式中,有几个关键点需要我们特别注意:
1. 纵坐标差与横坐标差:在计算斜率时,我们关注的是两点间纵坐标和横坐标的变化量,而不是它们的绝对值。这意味着,无论我们如何选择点的顺序(即A在前还是B在前),只要保持纵坐标差和横坐标差的符号一致,计算出的斜率都是相同的。
2. 分母不为零:斜率公式中的分母是x₂ - x₁,这意味着两点间的横坐标不能相同。如果x₁ = x₂,那么分母将为零,斜率公式将失去意义。在这种情况下,我们称直线为“垂直线”,其斜率不存在(或者说,斜率为无穷大)。
3. 斜率的正负:斜率的正负取决于纵坐标差与横坐标差的符号。如果y₂ > y₁且x₂ > x₁,或者y₂ < y₁且x₂ < x₁,那么斜率为正,表示直线从左下方向右上方倾斜;反之,如果y₂ > y₁且x₂ < x₁,或者y₂ < y₁且x₂ > x₁,那么斜率为负,表示直线从左上方向右下方倾斜。
四、斜率的应用:从几何到生活
斜率不仅是一个数学概念,它在现实生活中也有着广泛的应用。
1. 几何图形:在解析几何中,斜率用于描述直线、线段和曲线的倾斜程度。通过计算斜率,我们可以判断两条直线是否平行(斜率相等)或垂直(斜率互为相反数的倒数)。此外,斜率还帮助我们求解直线与坐标轴的交点、直线的方程等。
2. 物理运动:在物理学中,斜率常用于描述物体的运动状态。例如,在速度-时间图像中,斜率表示物体的加速度;在位移-时间图像中,斜率表示物体的速度。通过计算斜率,我们可以了解物体的运动规律。
3. 经济学:在经济学中,斜率常用于描述经济变量的关系。例如,在需求曲线中,斜率表示价格变动对需求量的影响程度;在供给曲线中,斜率表示成本变动对供给量的影响程度。通过计算斜率,我们可以分析市场供需关系的变化。
4. 工程设计:在工程设计中,斜率用于描述地形的起伏、道路的坡度等。通过计算斜率,我们可以确定道路的设计标准、排水系统的布局等。
五、斜率计算中的特殊情况
在计算斜率时,我们还需要注意一些特殊情况:
1. 水平线:如果直线是水平的,那么它不会上升也不会下降,因此斜率为零。这意味着,无论我们选择哪两个点来计算斜率,只要它们在同一水平线上,结果都将是零。
2. 垂直线:如果直线是垂直的,那么它将无限上升或下降,因此斜率不存在(或者说,斜率为无穷大)。在这种情况下,我们无法用斜率公式来计算斜率,因为分母将为零。
3. 重合点:如果我们选择的两个点是重合的,那么它们之间将没有距离可言,因此也无法计算斜率。在这种情况下,我们需要重新选择两个不同的点来计算斜率。
六、斜率与直线的方程
斜率不仅可以帮助我们描述直线的倾斜程度,还可以用于求解直线的方程。在解析几何中,直线的方程通常表示为y = mx + b的形式,其中m是斜率,b是截距(即直线与y轴的交点)。通过已知的两个点,我们可以先计算出斜率m,然后代入其中一个点的坐标求解截距b,从而得到直线的方程。
七、结语:斜率背后的数学之美
斜率,这个看似简单的数学概念,实际上蕴含着丰富的内涵和广泛的应用。它不仅是连接几何与代数的桥梁,更是我们认识世界、理解世界的重要工具。通过计算斜率,我们可以量化直线的倾斜程度,分析物体的运动状态,预测经济变量的变化趋势,甚至指导工程设计的实践。在这个过程中,我们不仅能够感受到数学的魅力,更能够领略到数学在解决实际问题中的巨大价值。
因此,当我们再次面对“两点怎么求斜率”的问题时,不妨将其视为一次探索数学奥秘的旅程。在这个过程中,我们将学会如何运用数学工具解决实际问题,如何运用数学思维分析问题本质。而这一切的起点,就是那两个看似平凡却又充满无限可能的点。
- 上一篇: 揭秘磷钾肥:强大作用与显著功效
- 下一篇: 如何找到并使用Word中的公式编辑器
-
 2x的导数求解,一看就懂!资讯攻略11-06
2x的导数求解,一看就懂!资讯攻略11-06 -
 轻松学会坡度计算方法资讯攻略11-07
轻松学会坡度计算方法资讯攻略11-07 -
 揭秘:斜率公式的神秘面纱资讯攻略01-23
揭秘:斜率公式的神秘面纱资讯攻略01-23 -
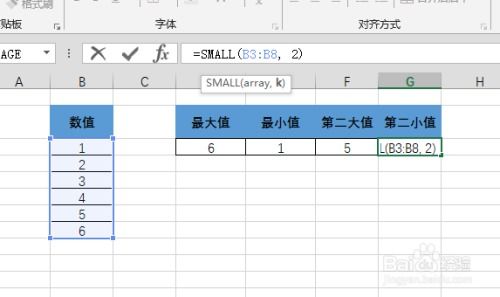 Excel中轻松求解最小值的函数方法资讯攻略12-05
Excel中轻松求解最小值的函数方法资讯攻略12-05 -
 Matlab方程求解资讯攻略12-06
Matlab方程求解资讯攻略12-06 -
 探寻三角函数解析式的求解策略资讯攻略11-25
探寻三角函数解析式的求解策略资讯攻略11-25












