揭秘:圆形面积计算公式全解析
圆形,作为几何学中最为基础且广泛应用的形状之一,其面积的计算是数学、物理、工程等多个领域不可或缺的知识点。本文将深入探讨圆形的面积计算公式,从其定义出发,逐步推导出著名的圆面积公式,并结合实例和实际应用,帮助读者全面理解这一基本概念。

圆形的定义与基本属性
圆形,简单来说,是一个平面上所有与给定点(称为圆心)距离相等的点的集合。这个给定的距离,我们称之为半径,通常用字母r表示。圆的直径则是穿过圆心、两端都在圆上的线段,其长度是半径的两倍,即2r。

圆形的特性之一是其完美的对称性,无论是中心对称还是轴对称,圆形都表现得淋漓尽致。这种对称美不仅让圆形成为自然界和人造物体中常见的形态,也使其在数学和物理中扮演着重要角色。
圆形面积的探索与推导
圆形面积的计算,看似简单,实则蕴含了深刻的数学原理。早在古希腊时期,数学家们就开始了对圆面积的探索。阿基米德,这位被誉为“力学之父”的伟大科学家,就利用分割、重组的方法,近似地计算出了圆的面积。
现代数学中,我们通常使用积分的方法来精确计算圆的面积。但在此之前,让我们通过一个更为直观的方式——几何方法,来推导圆的面积公式。
想象一个圆,我们将其分割成若干个小扇形,当这些小扇形的数量足够多时,它们可以近似地看作是一个个小的等腰三角形。每个三角形的底边长度可以看作是圆上的一段小弧,而高则是圆的半径r。将这些三角形拼合起来,就形成了一个近似的平行四边形,其底边长度接近圆的周长的一半(πr),高仍为r。
根据平行四边形的面积公式(底乘以高),我们可以得到这个近似图形的面积为πr²/2 * 2 = πr²。随着分割的扇形数量无限增加,这个近似值将越来越接近圆的真实面积。因此,我们得出结论:圆的面积A等于π乘以半径r的平方,即A = πr²。
π的奥秘
在上述公式中,π(圆周率)是一个至关重要的常数,它表示圆的周长与直径的比值。π的值约为3.14159...,是一个无理数,意味着它不能表示为两个整数的比。尽管π的精确值无法完全确定,但数学家们已经利用现代计算技术,计算出了π的上亿位小数。
π不仅是计算圆面积的关键,它还广泛出现在数学、物理、工程等学科的各个领域。从波动方程到量子力学,从电磁学到热力学,π的身影无处不在。甚至有人认为,宇宙的基本结构和性质可能与π的某些特性密切相关。
圆形面积计算的实际应用
圆形面积的计算公式,不仅具有理论价值,更在日常生活和工业生产中发挥着重要作用。
1. 建筑与设计
在建筑设计中,圆形常常被用作窗户、门洞、屋顶等元素的形状。设计师需要根据实际需求,计算出这些圆形元素的面积,以确保建筑的美观性和实用性。
2. 工程与制造
在机械工程中,齿轮、轴承等零部件的制造往往需要精确计算圆形的面积和周长。此外,在管道铺设、电缆铺设等工程中,圆形截面的管道和电缆因其良好的流动性和抗压能力而被广泛应用,其面积的计算对于确定材料用量和成本至关重要。
3. 物理学与天文学
在物理学中,圆形的面积计算涉及到电磁波的传播、光的衍射等现象。在天文学中,行星、恒星等天体的运动轨迹往往可以近似看作圆形或椭圆形,其面积的计算有助于研究天体的运动规律和相互作用。
4. 日常生活
圆形面积的计算还广泛应用于我们的日常生活中。比如,烹饪时计算圆形饼干的面积以确定烘烤时间;园艺中计算圆形花坛的面积以合理安排花卉种植;甚至在购买圆形地毯或桌布时,我们也需要根据房间或桌子的尺寸来计算所需面积。
圆形面积计算中的注意事项
在使用圆形面积公式进行计算时,需要注意以下几点:
确保给定的半径r是准确值,避免因测量误差导致的计算结果偏差。
理解π的近似值与实际值的差异,对于精度要求较高的计算,应使用更多位的π值。
在实际应用中,要考虑圆形物体的实际形状(如圆形花坛可能因土壤沉降而略微变形),以及测量工具的限制(如刻度尺的精度),这些因素都可能影响最终的计算结果。
结语
圆形的面积计算公式A = πr²,是数学中一个简单而深刻的定理。它不仅揭示了圆形这一基本几何形状的内在属性,更在科学研究、工程设计、日常生活等多个领域发挥着不可替代的作用。通过深入理解和应用这一公式,我们可以更好地认识世界,解决实际问题,推动科学技术的进步和发展。希望本文能够帮助读者全面理解圆形面积的计算公式,激发对数学和科学的兴趣与热爱。
- 上一篇: 职称里,“designation”究竟意味着什么?
- 下一篇: 如何快速查询本地停电通知信息
-
 如何计算9寸披萨的面积资讯攻略11-13
如何计算9寸披萨的面积资讯攻略11-13 -
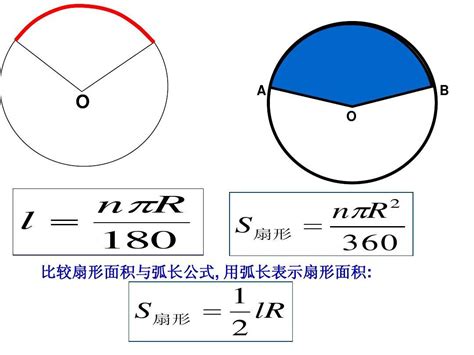 扇形面积如何计算?资讯攻略11-27
扇形面积如何计算?资讯攻略11-27 -
 直角三角形的面积该怎么计算?求公式!资讯攻略10-27
直角三角形的面积该怎么计算?求公式!资讯攻略10-27 -
 揭秘:半衰期计算公式全解析资讯攻略12-03
揭秘:半衰期计算公式全解析资讯攻略12-03 -
 如何计算直角三角形的面积?使用什么公式?资讯攻略10-24
如何计算直角三角形的面积?使用什么公式?资讯攻略10-24 -
 球的表面积计算公式及详解资讯攻略11-25
球的表面积计算公式及详解资讯攻略11-25











