揭秘二次函数的顶点:数学之美的隐藏角落
在数学的世界里,二次函数作为一类重要的函数类型,不仅在代数领域占据核心地位,更在几何、物理乃至实际应用中展现出广泛的应用价值。而谈及二次函数,一个绕不开的话题便是其顶点。顶点,作为二次函数图像上的特殊点,不仅是函数性质的关键体现,也是解决相关问题的关键所在。本文将从多个维度出发,深入探讨二次函数的顶点,揭示其内在的数学魅力。

一、二次函数的定义与基本形式
二次函数,顾名思义,其函数值y与自变量x之间满足二次方的关系,即形如y=ax²+bx+c(a≠0)的函数。其中,a、b、c为常数,且a不为0,以确保函数确实为二次函数。根据a的正负,二次函数的开口方向有所不同:当a>0时,函数图像开口向上;当a<0时,函数图像开口向下。
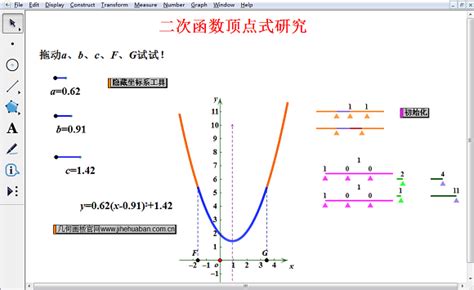
二、顶点的几何意义
二次函数的图像是一条抛物线,而顶点则是这条抛物线的最高点(当a>0时)或最低点(当a<0时)。在几何上,顶点位于抛物线的对称轴上,是抛物线上距离其两侧任意等距离点最近的一点。因此,顶点不仅代表了抛物线的最高或最低位置,还反映了抛物线的对称性质。

三、顶点的坐标公式
二次函数的顶点坐标可以通过公式直接求得,这是解决相关问题最为直接且有效的方法。对于一般形式的二次函数y=ax²+bx+c,其顶点坐标为(-b/2a, c-b²/4a)。这个公式揭示了顶点坐标与二次函数系数之间的内在联系。具体来说:
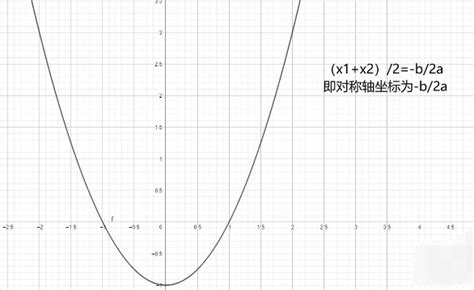
横坐标(-b/2a):它反映了抛物线的对称轴位置,是抛物线左右对称的分界线。
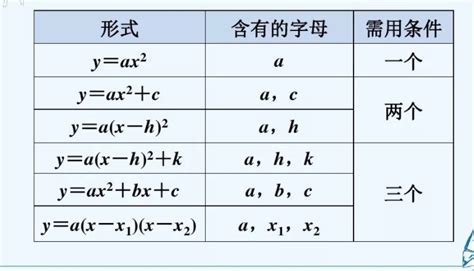
纵坐标(c-b²/4a):它代表了顶点的高度,即抛物线的最高或最低值。
通过这个公式,我们可以迅速定位二次函数的顶点,进而分析抛物线的整体形态。
四、顶点的代数性质
从代数的角度来看,顶点坐标的求解过程实际上是对二次函数进行配方的过程。将y=ax²+bx+c转化为顶点式y=a(x+b/2a)²+(c-b²/4a),不仅便于我们直接读出顶点坐标,还使得二次函数的性质更加直观清晰。配方的过程,实质上是对二次函数进行因式分解的一种特殊形式,它体现了数学中的转化思想,即将复杂问题简化为已知或更易处理的形式。
五、顶点的应用实例
二次函数的顶点在实际问题中有着广泛的应用。例如,在物理学中,抛物运动(如投掷物体、喷泉等)的轨迹就是一条抛物线,其顶点坐标可以帮助我们确定物体的最高点位置及其速度等信息。在经济学中,成本函数、收益函数等往往也是二次函数的形式,通过分析其顶点,我们可以找到成本最低或收益最大的生产量。此外,在工程设计、建筑设计等领域,抛物线的形状被广泛应用于天线设计、桥梁结构等,顶点的确定对于确保结构的稳定性和美观性至关重要。
六、顶点的动态变化
当二次函数的系数a、b、c发生变化时,其顶点的位置也会随之改变。这为我们提供了一个动态观察二次函数性质的角度。例如,保持a不变,改变b或c的值,可以观察到抛物线在水平方向或垂直方向上的平移;而改变a的值,则会影响抛物线的开口大小和方向。这些变化,通过顶点坐标的实时更新,得以直观展现。
七、顶点与极值问题
在求解二次函数的极值问题时,顶点坐标扮演了至关重要的角色。由于二次函数在其定义域内只有一个极值点(最高点或最低点),因此该极值点必然就是抛物线的顶点。通过计算顶点坐标,我们可以直接得出二次函数的最大值或最小值,这对于解决最优化问题具有重要意义。
八、顶点的几何作图法
除了通过公式计算顶点坐标外,我们还可以通过几何作图法来找到二次函数的顶点。具体方法是:首先画出二次函数的图像(可以通过选取几个关键点并连线来完成),然后找到抛物线的对称轴(通过观察图像或计算得出),最后在对称轴上找到距离抛物线两侧等距离的点,该点即为顶点。虽然这种方法不如公式法精确快捷,但它能够让我们更加直观地感受到抛物线的对称性和顶点的位置。
九、顶点与函数变换
二次函数的顶点还与函数的变换密切相关。通过对二次函数进行平移、伸缩等变换操作,可以得到新的二次函数。这些变换操作不仅改变了原函数的图像形态,也相应地改变了顶点的位置。例如,将y=ax²沿x轴平移h个单位,得到的新函数为y=a(x-h)²,其顶点坐标为(h,0);若再将此函数沿y轴平移k个单位,则得到的新函数为y=
- 上一篇: 如何设置朋友圈动态背景
- 下一篇: 如何正确使用眼霜的有效手法
-
 揭秘:顶点公式的详细解析资讯攻略11-22
揭秘:顶点公式的详细解析资讯攻略11-22 -
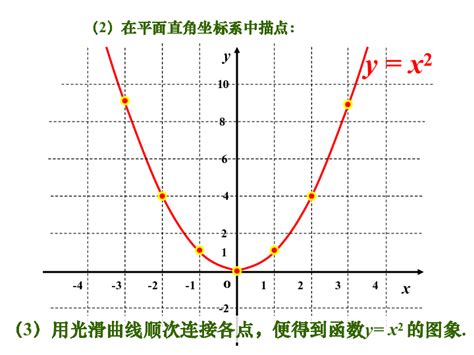 深入解析二次函数图像及其核心性质资讯攻略10-29
深入解析二次函数图像及其核心性质资讯攻略10-29 -
 揭秘三次函数的图像特征与性质资讯攻略11-07
揭秘三次函数的图像特征与性质资讯攻略11-07 -
 揭秘二次根式性质的奥秘资讯攻略11-19
揭秘二次根式性质的奥秘资讯攻略11-19 -
 双曲线的顶点坐标如何求解资讯攻略11-10
双曲线的顶点坐标如何求解资讯攻略11-10 -
 如何计算直角三角形的斜边长度资讯攻略11-17
如何计算直角三角形的斜边长度资讯攻略11-17