揭秘三次函数的图像特征与性质
三次函数的图像和性质深度解析

在数学的广阔天地里,三次函数以其独特的魅力和复杂性吸引着无数探索者的目光。作为一类重要的非线性函数,三次函数不仅在数学理论上占据重要地位,还在物理、工程、经济等多个领域有着广泛的应用。本文将深入探讨三次函数的图像和性质,带领读者走进这一奇妙的世界。
一、三次函数的基本形式
三次函数的一般形式为:
f(x) = ax³ + bx² + cx + d
其中,a、b、c、d为实数,且a ≠ 0(若a=0,则函数退化为二次函数)。这个表达式看似简单,却蕴含着丰富的数学内涵。
二、三次函数的图像特征
1. 图像的对称性
三次函数的图像通常不具有轴对称性,但具有中心对称性。当a>0时,图像呈“S”形,且开口向上;当a<0时,图像呈反“S”形,且开口向下。这种中心对称性体现在:如果点(x₀, y₀)在图像上,那么点(-x₀-2b/3a, -y₀)也在图像上。
2. 极值点
三次函数在其定义域内至少有一个极值点,且最多有两个。这些极值点可以通过求导并令导数等于0来找到。具体地,对f(x)求导得:
f'(x) = 3ax² + 2bx + c
令f'(x) = 0,解得x的值即为极值点的横坐标。将x值代入原函数f(x),即可求得极值点的纵坐标。
3. 拐点
三次函数在其定义域内还可能存在拐点,即图像上凹凸性发生变化的点。拐点的存在与否以及位置,取决于二阶导数f''(x)的符号变化。当f''(x)从正变为负或从负变为正时,对应的x值即为拐点的横坐标。
三、三次函数的性质
1. 单调性
三次函数的单调性取决于其一阶导数f'(x)的符号。当f'(x)>0时,函数在该区间内单调递增;当f'(x)<0时,函数在该区间内单调递减。通过求解f'(x)=0得到的解,可以将定义域划分为若干个区间,每个区间内函数具有相同的单调性。
2. 有界性
三次函数在其定义域内通常是无界的,即当x趋向于正无穷或负无穷时,f(x)也趋向于正无穷或负无穷(取决于a的符号)。然而,在某些特定情况下,如当a<0且b²-3ac>0时,函数在某一区间内可能是有界的。
3. 奇偶性
三次函数通常不具有奇偶性,即f(-x) ≠ f(x)且f(-x) ≠ -f(x)。但有一种特殊情况需要注意:当b=c=0时,函数f(x)=ax³+d变为奇函数(若d=0)或偶函数加奇函数的形式(若d≠0,但此时仍不具有纯粹的奇偶性)。
4. 零点与方程
三次方程的求解是数学中的一个经典问题。虽然三次方程没有像二次方程那样简单的求根公式,但可以通过卡尔丹公式或数值方法找到其根。三次函数的零点对应于三次方程的解,它们在图像上表现为与x轴的交点。
四、三次函数的应用实例
1. 物理学中的应用
在物理学中,三次函数常用于描述某些物理量的变化规律。例如,在弹性力学中,当物体受到非线性弹性力作用时,其位移与力的关系可能呈现为三次函数的形式。此外,在热力学、电磁学等领域中,三次函数也扮演着重要角色。
2. 工程学中的应用
在工程学中,三次函数常用于拟合实验数据、设计曲线形状等。例如,在机械设计中,为了优化零件的轮廓形状以提高其性能,工程师可能会使用三次函数来描述零件的轮廓线。此外,在土木工程、航空航天等领域中,三次函数也有着广泛的应用。
3. 经济学中的应用
在经济学中,三次函数常用于描述某些经济变量的变化趋势。例如,在需求函数中,当需求量与价格之间的关系呈现非线性变化时,可以使用三次函数来近似描述这种关系。此外,在成本函数、收益函数等经济模型中,三次函数也常被用作分析工具。
五、三次函数的图像绘制与性质分析技巧
1. 图像绘制技巧
绘制三次函数的图像时,可以先求出函数的极
- 上一篇: 家常美味银耳羹制作教程
- 下一篇: 如何让女性乳房增大?
-
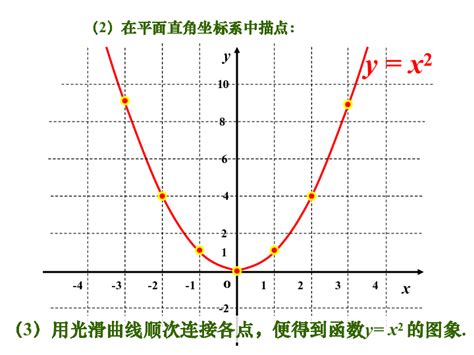 深入解析二次函数图像及其核心性质资讯攻略10-29
深入解析二次函数图像及其核心性质资讯攻略10-29 -
 揭秘:函数拐点的奥秘资讯攻略11-22
揭秘:函数拐点的奥秘资讯攻略11-22 -
 揭秘二次函数的顶点:数学之美的隐藏角落资讯攻略11-06
揭秘二次函数的顶点:数学之美的隐藏角落资讯攻略11-06 -
 揭秘:arcsinx与sinx分之一,它们真的是等价的吗?资讯攻略10-31
揭秘:arcsinx与sinx分之一,它们真的是等价的吗?资讯攻略10-31 -
 掌握指数函数!必知的8个基本公式资讯攻略11-22
掌握指数函数!必知的8个基本公式资讯攻略11-22 -
 什么是高等数学入门中的曲线拐点?如何求解?资讯攻略11-20
什么是高等数学入门中的曲线拐点?如何求解?资讯攻略11-20












