深入解析二次函数图像及其核心性质

二次函数是数学中一个极其重要的概念，尤其在代数和解析几何领域扮演着不可或缺的角色。二次函数的图像，即抛物线，不仅具有优美的几何形态，还蕴含着丰富的数学性质。这些性质不仅在理论上具有重要意义，还在实际应用中发挥着巨大作用。下面，我们从多个维度深入探讨二次函数的图像和性质。

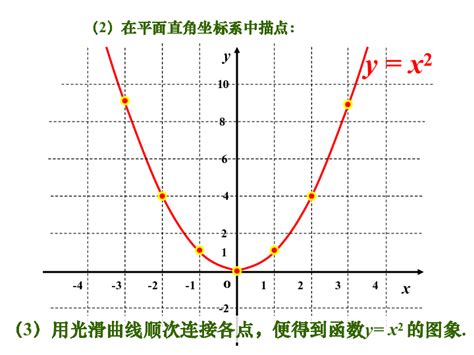
一、二次函数的基本形式与图像

二次函数的一般形式为f(x) = ax^2 + bx + c，其中a、b、c为实数，且a ≠ 0。这个表达式描述了平面直角坐标系中一个变量的平方与另一个变量之间的线性关系，并附加一个常数项。

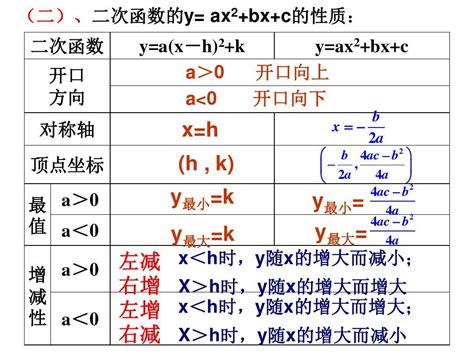
根据a的正负，二次函数的图像会有不同的开口方向。当a > 0时，抛物线开口向上，表示函数值随着x的增大而先减小后增大；当a < 0时，抛物线开口向下，表示函数值随着x的增大而先增大后减小。这一性质是二次函数图像最为直观的特征之一。

二、二次函数的顶点与对称轴

二次函数的顶点是其图像上的最低点（当a > 0时）或最高点（当a < 0时），也是函数值取得极值（最大或最小）的点。顶点坐标可以通过公式(-b/2a, c - b^2/4a)计算得到。这一公式不仅简洁，而且揭示了顶点与二次函数系数之间的直接关系。

对称轴是过顶点且与抛物线对称的直线，其方程为x = -b/2a。由于抛物线关于对称轴对称，因此在对称轴两侧，函数值具有相同的增减性。这一性质使得我们可以利用对称轴简化二次函数的分析和计算。

三、二次函数的单调性

单调性是函数在定义域内某一区间上单调增加或单调减少的性质。对于二次函数，其单调性取决于对称轴的位置以及a的正负。

当a > 0时，抛物线开口向上，函数在对称轴左侧单调递减，在对称轴右侧单调递增；当a < 0时，抛物线开口向下，函数在对称轴左侧单调递增，在对称轴右侧单调递减。这一性质是二次函数在实际应用中判断函数值大小、求解最值等问题的基础。

四、二次函数的最大值与最小值

二次函数的最大值或最小值发生在顶点处。当a > 0时，函数取得最小值，即顶点处的函数值；当a < 0时，函数取得最大值，同样为顶点处的函数值。

这一性质在解决实际问题时具有广泛应用。例如，在经济学中，可以利用二次函数求解成本最低或利润最大的生产量；在物理学中，可以求解抛体运动的最高点或最低点等。

五、二次函数与方程、不等式的关系

二次函数与一元二次方程、一元二次不等式之间存在着密切的联系。一元二次方程ax^2 + bx + c = 0的解就是二次函数f(x) = ax^2 + bx + c与x轴交点的横坐标。因此，方程根的个数、性质以及求解方法都与二次函数的图像密切相关。

同样地，一元二次不等式ax^2 + bx + c > 0（或< 0）的解集也可以通过分析二次函数的图像得到。当不等式表示的区域在抛物线上方时，解集为抛物线开口方向所指的区域；当不等式表示的区域在抛物线下方时，解集为抛物线开口方向相反的区域。这一性质为求解不等式提供了直观、简洁的方法。

六、二次函数的实际应用

二次函数的图像和性质在现实生活中具有广泛的应用。例如，在建筑设计中，可以利用二次函数求解抛物面天线的形状和尺寸；在物理学中，可以利用二次函数描述抛体运动的轨迹；在经济学中，可以利用二次函数求解成本函数、收益函数和利润函数等。

此外，二次函数还与优化问题密切相关。在许多实际问题中，我们需要找到使目标函数取得最大值或最小值的变量取值。这些目标函数往往是二次函数或可以近似为二次函数。因此，利用二次函数的性质求解优化问题具有广泛的实际意义。

七、二次函数的变换与几何意义

二次函数可以通过平移、伸缩等变换得到新的二次函数。这些变换不仅改变了函数的图像和性质，还揭示了不同二次函数之间的内在联系。

例如，将二次函数f(x) = ax^2沿x轴平移h个单位，得到新的函数f(x) = a(x - h)^2；沿y轴平移k个单位，得到f(x) = ax^2 + k。这些平移变换不改变抛物线的开口方向和大小，只改变其位置。

伸缩变换则通过改变系数a、b、c的值来实现。例如，将二次函数f(x) = ax^2的系数a扩大（或缩小）k倍，得到新的函数f