凸四边形和凹四边形分别是什么?
凸四边形和凹四边形的定义在几何学中占据着重要的地位,它们分别代表了四边形性质的两种基本分类。了解这两种四边形的定义及其特性,不仅有助于深化对几何图形的认识,还能在实际应用中发挥重要作用。
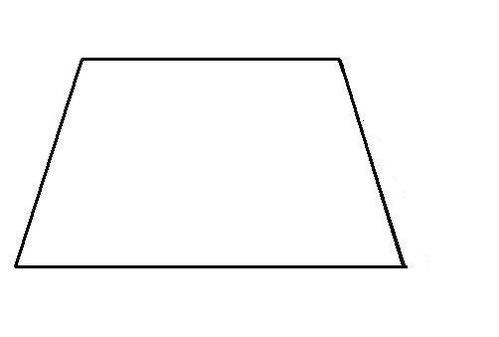
首先,我们来探讨凸四边形的定义。凸四边形,顾名思义,是指所有内角均小于180度的四边形。换句话说,如果一个四边形的所有顶点都位于其任意一边的同侧,那么这个四边形就是凸四边形。在凸四边形中,任意一条对角线都可以将四边形划分为两个三角形,这两个三角形的内角和均为180度,且四边形的总内角和为360度。此外,凸四边形的所有外角也都是凸角,即小于180度的角。常见的凸四边形有正方形、长方形、平行四边形、梯形等。这些四边形在日常生活中随处可见,如房间的墙壁、门窗的框架、书本的形状等,都是凸四边形的典型例子。

正方形作为凸四边形的一种,具有所有边等长且所有内角均为直角的特性。长方形则与正方形类似,但长和宽可以不相等,其内角也均为直角。平行四边形则要求两组对边分别平行且等长,但内角不一定为直角。梯形则是一种特殊的平行四边形,它只有一组对边平行,这组平行边被称为梯形的上底和下底,而不平行的两边则被称为梯形的腰。

接下来,我们转向凹四边形的定义。与凸四边形相反,凹四边形至少有一个内角大于180度。这意味着凹四边形的至少一个顶点会位于其某条边所在直线的另一侧。在凹四边形中,由于存在大于180度的内角,因此不能简单地通过一条对角线将其划分为两个三角形。凹四边形的总内角和仍然为360度,但由于存在凹角(大于180度的角),其外角可能会小于0度或大于180度。需要注意的是,虽然凹四边形在日常生活中的应用不如凸四边形广泛,但在某些特定领域,如建筑设计、艺术创作等,凹四边形却能够展现出独特的魅力和价值。

为了更直观地理解凸四边形和凹四边形的区别,我们可以通过一些实例进行对比。例如,一个标准的矩形房间可以看作是一个凸四边形,因为其所有内角均为直角,且所有顶点都位于房间的同一侧。而如果一个房间的设计中包含了一个向内凹陷的角落,那么这个角落就可以看作是一个凹角,整个房间的形状也就变成了一个凹四边形。在艺术创作中,画家可能会利用凹四边形的特性来创造具有视觉冲击力的作品,如通过描绘一个具有凹角的建筑物或景观来增强画面的层次感和深度感。
此外,凸四边形和凹四边形在几何学中还有一些重要的性质和定理。例如,凸四边形的外角和定理指出,凸四边形的四个外角之和等于360度。这一性质在解决与凸四边形相关的问题时非常有用。而对于凹四边形来说,由于其存在凹角,因此外角和定理不再适用。但是,凹四边形仍然具有一些独特的性质,如可以通过延长其凹边来构造新的几何图形,并据此推导出一些有用的结论。
在解决与凸四边形和凹四边形相关的问题时,我们还需要注意一些常见的误区。例如,有些人可能会错误地认为只有所有边都相等的四边形才是凸四边形,或者认为所有内角都大于180度的四边形才是凹四边形。这些误解都源于对凸四边形和凹四边形定义的不准确理解。实际上,凸四边形和凹四边形的分类主要基于其内角的大小和顶点的位置关系,而与边的长度无关。
综上所述,凸四边形和凹四边形是几何学中两种基本的四边形分类。凸四边形具有所有内角均小于180度的特性,而凹四边形则至少有一个内角大于180度。了解这两种四边形的定义及其特性不仅有助于深化对几何图形的认识,还能在实际应用中发挥重要作用。无论是在建筑设计、艺术创作还是数学研究中,凸四边形和凹四边形都扮演着不可或缺的角色。因此,我们应该认真学习并掌握这两种四边形的相关知识,以便更好地应用它们来解决实际问题。
- 上一篇: 简易爱心折纸教程:一步步学会
- 下一篇: 揭秘:昭阳公主背后的历史原型究竟是谁?
-
 四边形定义全解析资讯攻略11-05
四边形定义全解析资讯攻略11-05 -
 平行四边形对角线长度快速计算公式资讯攻略11-02
平行四边形对角线长度快速计算公式资讯攻略11-02 -
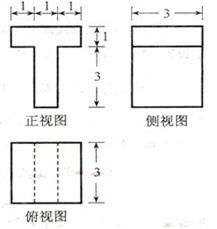 四棱柱的侧面展开图是什么样子的图形?资讯攻略11-03
四棱柱的侧面展开图是什么样子的图形?资讯攻略11-03 -
 如何从图片中准确识别长方形的长和宽资讯攻略11-06
如何从图片中准确识别长方形的长和宽资讯攻略11-06 -
 正方形周长计算公式详解资讯攻略10-31
正方形周长计算公式详解资讯攻略10-31 -
 如何计算一个数的平方资讯攻略11-14
如何计算一个数的平方资讯攻略11-14












