四边形定义全解析

四边形是几何学中的一个基本概念，它指的是具有四条边和四个顶点的平面图形。在探讨四边形的概念时，我们需要从定义出发，逐步深入，了解其分类、性质以及在实际生活中的应用。

首先，明确四边形的定义是关键。四边形是由不在同一条直线上的四条线段首尾顺次相接所组成的平面图形。这四个线段被称为四边形的边，它们相交的点被称为四边形的顶点。四边形具有四条边和四个内角，这些内角的和总是等于360度，这是四边形的一个重要性质。

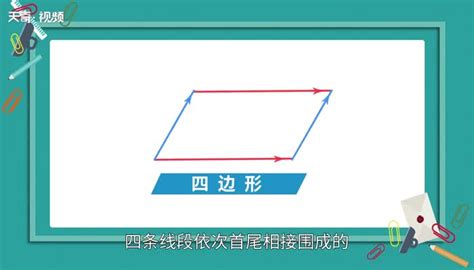
根据四边形的边长和角度的不同，我们可以将其分为多种类型。最常见的是平行四边形，它的定义是两组对边分别平行。平行四边形有许多特殊的性质，比如对边相等、对角相等、对角线互相平分等。在平行四边形中，如果有一个角是直角，那么它就变成了矩形；如果所有的角都是直角，那么它就是正方形，正方形是一种特殊的矩形，它的四条边都相等。

除了平行四边形，还有梯形这一类别。梯形是指只有一组对边平行的四边形。根据另一组对边是否相等，梯形又可以进一步分为等腰梯形和不等腰梯形。等腰梯形的特点是两腰相等，不等腰梯形则没有这一性质。在梯形中，如果有一个角是直角，那么它就是直角梯形。

在四边形的世界中，还有一些特殊的四边形值得我们关注。菱形是一种四边相等的平行四边形，它的对角线互相垂直且平分每一组对角。菱形具有独特的对称性，使得它在许多设计中都非常受欢迎。另外，风筝形（也称菱形的一种特殊情况，但更广义上指对角线互相垂直但不相等的四边形）和等腰梯形也具有某种程度的对称性，这使得它们在建筑和艺术中有所应用。

当我们深入研究四边形的性质时，会发现它们与我们的生活息息相关。例如，四边形在建筑设计中的应用非常广泛。无论是房屋的结构设计，还是门窗的形状选择，都离不开对四边形性质的理解和运用。在建筑中，四边形因其稳定性和简洁性而被广泛采用。同时，四边形也在艺术创作中发挥着重要作用。艺术家们常常利用四边形的对称性和规则性来创造美丽的图案和作品。

此外，四边形在数学学习中也占据着重要地位。它是学生们从简单的几何图形过渡到复杂几何图形的一个桥梁。通过学习四边形，学生们可以掌握许多重要的几何概念和技能，如角度计算、边长测量、图形变换等。这些概念和技能不仅在数学学科中有着重要的应用价值，还可以帮助学生们更好地理解和解决其他学科中的问题。

在解决四边形问题时，我们经常会用到一些基本的几何定理和性质。例如，平行线的性质、三角形的性质以及相似和全等的判定等。这些定理和性质为我们提供了解决四边形问题的有力工具。同时，我们还需要掌握一些基本的几何作图方法，如直线的绘制、角的平分、线段的垂直平分等。这些作图方法可以帮助我们更直观地理解和解决四边形问题。

当然，在学习四边形的过程中，我们也需要注意一些容易混淆的概念和难点。例如，在判断一个四边形是否为平行四边形时，我们需要明确其定义和性质，并仔细分析题目给出的条件。另外，在计算四边形的面积和周长时，我们也需要熟练掌握各种计算公式和方法，并注意单位换算和精度控制等问题。

为了更好地理解和掌握四边形的概念，我们可以采用多种学习方法和策略。首先，我们可以通过观察和比较不同类型的四边形来加深对其特征的理解。例如，我们可以比较平行四边形和梯形的异同点，以及矩形和正方形的特殊性质等。其次，我们可以通过实际操作和实验来验证四边形的性质。例如，我们可以使用尺子和量角器来测量四边形的边长和角度，或者使用纸张和剪刀来制作不同形状的四边形等。这些实践活动不仅可以帮助我们更好地理解和掌握四边形的概念，还可以提高我们的动手能力和创造力。

最后，我们还需要注意将四边形的学习与其他学科相结合。例如，在物理学中，我们可以利用四边形的性质来分析物体的受力和运动情况；在地理学中，我们可以利用四边形来描述地形地貌和地理位置等。这种跨学科的学习方法不仅可以拓宽我们的视野和知识面，还可以帮助我们更好地理解和应用四边形的概念。

综上所述，四边形作为几何学中的一个基本概念，具有丰富的内涵和广泛的应用价值。通过学习四边形，我们可以掌握许多重要的几何概念和技能，并了解它们在实际生活中的应用。同时，我们还需要注意采用多种学习方法和策略来提高学习效果和创造力。希望这篇关于四边形概念的介绍能够帮助读者更全面地了解四边形，并在学习和生活中更好地应用它们。