揭秘C55的计算方法,轻松掌握!

在日常生活中,我们时常会遇到各种数学问题和概念,它们或简单或复杂,但无一不蕴含着无尽的魅力。今天,我们要深入探讨一个可能并不广为人知,但却在数学、统计学、计算机科学等多个领域中都扮演重要角色的数字——C55。那么,C55究竟是什么呢?它又是如何计算的呢?让我们一起踏上这场充满趣味和探索的旅程吧!

一、揭开C55的神秘面纱
首先,让我们来明确一下C55的定义。在数学中,C55通常指的是组合数中的一个特例,即从55个不同元素中选出55个元素的组合数。组合数,又称二项式系数,是数学中的一个基本概念,用于计算在有限个不同元素中取出若干个元素的所有可能组合的个数。它的计算公式为C(n, k) = n! / [k!(n - k)!],其中n表示总元素个数,k表示选取的元素个数,“!””表示阶乘运算,即一个数与它前面所有正整数的乘积。

二、C55的具体计算过程
现在,我们已经知道了C55是组合数的一个特例,并且掌握了组合数的计算公式。那么,接下来我们就来具体计算一下C55的值。
将n=55和k=55代入组合数的计算公式,我们得到:
C55 = 55! / [55!(55 - 55)!]
= 55! / (55! * 0!)
由于0的阶乘定义为1(即0! = 1),所以上式可以进一步简化为:
C55 = 55! / 55!
= 1
这个结果可能会让一些人感到惊讶,因为从直觉上看,从55个元素中选出55个元素应该有很多种不同的方式。然而,实际上当我们需要选取的元素个数与总元素个数相等时,就只有一种可能的方式,即选取所有的元素。因此,C55的值为1也就不足为奇了。
三、C55的深入解读与应用
虽然C55的计算结果看似简单,但它在数学、统计学和计算机科学等多个领域中都有着广泛的应用和深刻的内涵。
1. 数学领域:
组合数学:组合数学是研究离散结构和组合对象的数学分支,组合数是其中最基本的概念之一。C55作为组合数的一个特例,可以用来解释和证明一些组合数学中的定理和性质。
概率论:在概率论中,组合数常用来计算某些事件的概率。例如,在掷骰子、抽牌等随机试验中,我们可以利用组合数来计算出现某种特定结果的概率。虽然C55本身并不直接用于概率计算,但理解组合数的概念和性质对于深入掌握概率论是非常重要的。
2. 统计学领域:
抽样调查:在统计学中,抽样调查是一种常用的数据收集方法。当需要从总体中选取一部分样本进行研究时,我们可以利用组合数来计算不同的抽样方式。虽然在实际应用中,我们很少会遇到需要选取与总体数量相等的样本的情况,但理解组合数的概念和计算方法对于设计合理的抽样方案仍然是非常重要的。
数据分析:在数据分析中,我们经常需要处理大量的数据并提取有用的信息。组合数可以用来计算数据集中不同元素之间的组合关系,从而帮助我们发现数据中的规律和模式。
3. 计算机科学领域:
算法设计:在计算机科学中,算法设计是一个重要的研究方向。许多算法都涉及到对数据的组合和排列操作。理解组合数的概念和计算方法可以帮助我们设计更高效的算法来解决实际问题。
信息编码:在信息编码领域,组合数常被用来设计各种编码方案。例如,在二进制编码中,我们可以利用组合数来计算不同长度的二进制串的数量,从而设计出具有特定性质的编码方案。
四、C55的趣味拓展
除了在数学、统计学和计算机科学等领域中的应用外,C55还可以引发一些有趣的思考和拓展。
数学游戏:我们可以设计一些基于组合数的数学游戏,如猜数字、组合拼图等。这些游戏不仅可以锻炼我们的思维能力和数学素养,还可以让我们在轻松愉快的氛围中感受到数学的魅力。
生活应用:虽然C55本身并不直接用于解决日常生活中的问题,但理解组合数的概念和性质可以帮助我们更好地理解和分析一些生活现象。例如,在购物时,我们可以利用组合数来计算不同商品组合的价格和优惠情况;在安排活动时,我们可以利用组合数来规划不同的活动方案和参与人员组合等。
五、结语
通过本文的介绍和探讨,相信大家对C55有了更深入的了解和认识。虽然C55的计算结果看似简单,但它在数学、统计学和计算机科学等多个领域中都有着广泛的应用和深刻的内涵。理解并掌握组合数的概念和计算方法对于我们深入掌握这些学科的知识和方法是非常重要的。同时,C55也可以引发我们对于一些有趣问题的思考和拓展,让我们在探索数学的奥秘中感受到无尽的乐趣和魅力。希望这篇文章能够激发大家对数学的兴趣和热情,让我们一起在数学的世界里遨游吧!
- 上一篇: 解锁收纳挑战,红色妖姬完美通关秘籍!
- 下一篇: DIY冰淇淋制作指南
-
 掌握CAD技巧:轻松计算面积的方法揭秘资讯攻略11-26
掌握CAD技巧:轻松计算面积的方法揭秘资讯攻略11-26 -
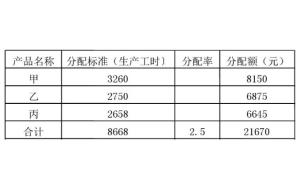 揭秘:轻松掌握分配率的计算方法资讯攻略11-24
揭秘:轻松掌握分配率的计算方法资讯攻略11-24 -
 揭秘:轻松掌握耗电量计算方法资讯攻略01-29
揭秘:轻松掌握耗电量计算方法资讯攻略01-29 -
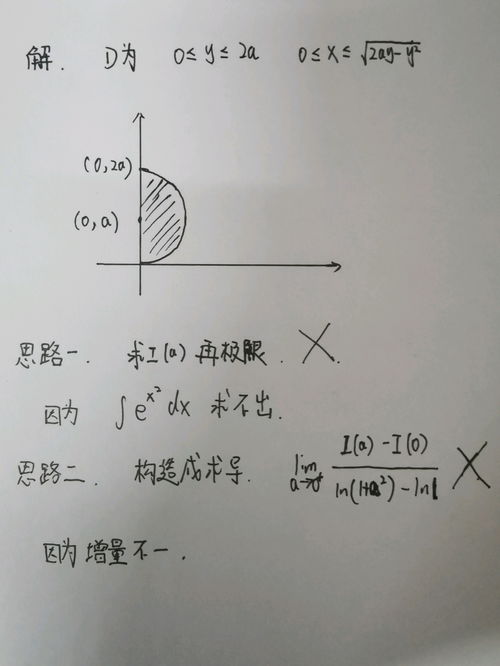 揭秘二重积分的计算方法,并通过例题轻松掌握!资讯攻略01-18
揭秘二重积分的计算方法,并通过例题轻松掌握!资讯攻略01-18 -
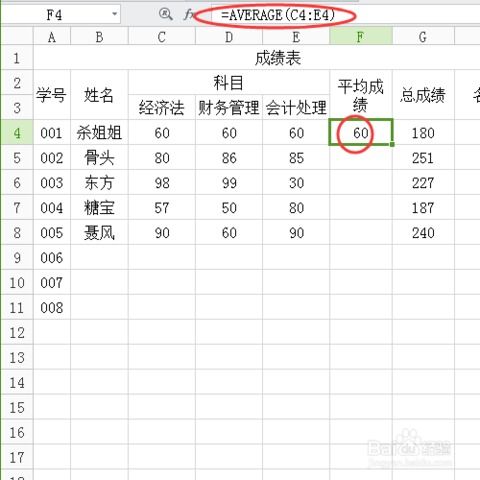 揭秘:轻松掌握平均数的计算方法资讯攻略10-28
揭秘:轻松掌握平均数的计算方法资讯攻略10-28 -
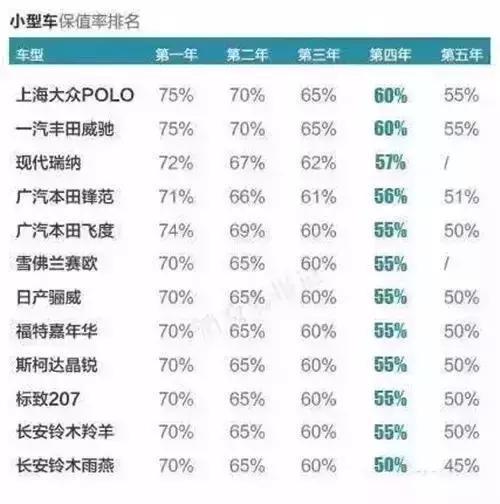 揭秘汽车折旧计算秘籍:轻松掌握爱车价值变化!资讯攻略11-26
揭秘汽车折旧计算秘籍:轻松掌握爱车价值变化!资讯攻略11-26












