揭秘二重积分的计算方法,并通过例题轻松掌握!
二重积分是多元微积分中的一个重要概念,它是对平面区域内的一个函数进行两次积分的过程。简单来说,二重积分可以理解为对某一平面区域上的函数值进行面积加权求和。这个过程涉及到对函数在不同区间和区域内进行积分,可以计算出平面图形的面积、质量、体积等多种物理量。接下来,我们将从二重积分的定义、计算方法、解题步骤以及一个简单例题等方面,详细介绍如何计算二重积分。
一、二重积分的定义
二重积分可以看作是对定义在平面区域D上的二元函数f(x,y)的一种积分。其物理意义可以理解为,对于某个平面区域D,其上的每一点(x,y)都对应一个函数值f(x,y),通过对这些函数值进行加权求和(即积分),可以得到一个总的值。这个值在物理学中可能代表质量、能量、电荷等。
从数学表达式上看,二重积分可以表示为:

∬_D f(x,y) dxdy
其中,D表示积分区域,f(x,y)是被积函数,dxdy表示对x和y同时进行微分。
二、二重积分的计算方法
二重积分的计算方法主要有两种:直角坐标系下的计算和极坐标系下的计算。这里我们主要介绍直角坐标系下的计算方法。
1. 直角坐标系下的二重积分
在直角坐标系下,二重积分可以看作是先对y进行积分,再对x进行积分(或者先对x积分,再对y积分),即:
∬_D f(x,y) dxdy = ∫_a^b dx ∫_φ₁(x)^φ₂(x) f(x,y) dy
或者
∬_D f(x,y) dxdy = ∫_c^d dy ∫_ψ₁(y)^ψ₂(y) f(x,y) dx
其中,a,b是x的取值范围,c,d是y的取值范围,φ₁(x), φ₂(x)和ψ₁(y), ψ₂(y)分别是积分区域的边界曲线方程。
2. 选择积分次序
在选择积分次序时,我们需要根据积分区域的形状和被积函数的特性来确定。一般来说,如果积分区域是一个矩形或者其边界曲线可以比较容易地表示为x或y的函数,那么我们就可以选择先对另一个变量进行积分。
3. 计算定积分
确定了积分次序和积分区间后,我们就可以按照定积分的计算方法来计算二重积分了。这通常涉及到对被积函数进行换元、分部积分等操作。
三、解题步骤
1. 确定积分区域:首先,我们需要明确题目中给出的积分区域D。这通常是一个由几条曲线围成的平面区域。
2. 选择积分次序:根据积分区域的形状和被积函数的特性,选择一个合适的积分次序。
3. 写出积分表达式:根据选择的积分次序和积分区域,写出二重积分的表达式。
4. 计算定积分:按照定积分的计算方法,计算出二重积分的值。
四、简单例题
例题:计算二重积分 ∬_D (x+y) dxdy,其中D是由直线x=0, y=0, x+y=1所围成的三角形区域。
解题步骤:
1. 确定积分区域:
积分区域D是由直线x=0, y=0, x+y=1所围成的三角形区域。这个三角形的三个顶点分别是(0,0),(1,0)和(0,1)。
2. 选择积分次序:
由于积分区域D是一个三角形,其边界曲线可以比较容易地表示为x或y的函数,因此我们可以选择先对y进行积分,再对x进行积分。
3. 写出积分表达式:
根据选择的积分次序和积分区域,我们可以写出二重积分的表达式:
∬_D (x+y) dxdy = ∫_0^1 dx ∫_0^(1-x) (x+y) dy
4. 计算定积分:
接下来,我们按照定积分的计算方法来计算这个二重积分:
∫_0^1 dx ∫_0^(1-x) (x+y) dy
= ∫_0^1 dx [xy + 0.5y²]|_0^(1-x)
= ∫_0^1 dx [x(1-x) + 0.5(1-x)²]
= ∫_0^1 (x - x² + 0.5 - x + 0.5x²) dx
= ∫_0^1 (0.5 - 0.5x²) dx
= [0.5x - (1/6)x³]|_0^1
= 0.5 - 1/6
= 1/3
因此,这个二重积分的值是1/3。
通过这个例题,我们可以看到,计算二重积分的关键在于确定积分区域、选择积分次序、写出积分表达式以及计算定积分。只要掌握了这些步骤和方法,我们就可以解决各种形式的二重积分问题。同时,我们还需要注意被积函数的特性和积分区域的形状,以便选择合适的解题策略。
- 上一篇: 怎样制作桃罐头?
- 下一篇: 家常美味:地皮菜与鸡蛋的绝妙碰撞——地皮炒鸡蛋详细做法
-
 轻松掌握二重积分dxdy的计算方法资讯攻略10-24
轻松掌握二重积分dxdy的计算方法资讯攻略10-24 -
 掌握函数值域求解方法及经典例题解析资讯攻略11-07
掌握函数值域求解方法及经典例题解析资讯攻略11-07 -
 掌握第一类曲线积分的高效计算方法资讯攻略11-01
掌握第一类曲线积分的高效计算方法资讯攻略11-01 -
 揭秘二重感染:一探究竟的名词解释资讯攻略11-22
揭秘二重感染:一探究竟的名词解释资讯攻略11-22 -
 揭秘!轻松查询手机积分,玩转商城积分转赠技巧资讯攻略11-27
揭秘!轻松查询手机积分,玩转商城积分转赠技巧资讯攻略11-27 -
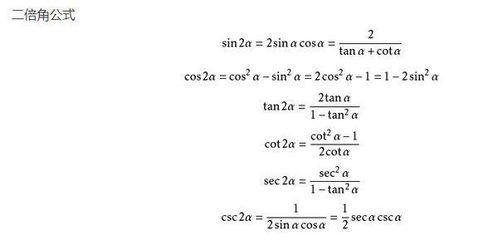 精通常见三角函数积分:公式推导与全面总结资讯攻略11-18
精通常见三角函数积分:公式推导与全面总结资讯攻略11-18