轻松掌握二重积分dxdy的计算方法

在探索数学的无垠宇宙中，二重积分如同一扇神秘而迷人的大门，引领我们穿梭于平面区域的奥秘之间。想象一下，你站在一片广袤无垠的二维平原上，手中握着一把能够衡量这片土地上每一寸土地“重量”或“价值”的神奇量尺——这就是二重积分。它不仅仅是一个数学概念，更是连接理论与实际、抽象与具象的桥梁。今天，就让我们一起踏上一场关于“二重积分dxdy怎么算”的奇妙旅程，解开它那既复杂又迷人的面纱。

一、二重积分的初印象：从平面到立体的跨越

在正式踏入二重积分的世界之前，不妨先回想一下一维世界中的定积分。定积分如同一位勤劳的工匠，能够计算出曲线下方与坐标轴围成的面积。而二重积分，则是这位工匠在二维空间中的升级版，它不仅能“看见”平面的宽度与高度，还能“感受”到这片平面下的“厚度”或“密度”。简而言之，二重积分帮助我们计算的是某一平面区域内某一函数值累积的总和，这个总和可能是面积、体积、质量、能量等多种物理量的数学表达。

二、揭开dxdy的神秘面纱：分步计算的智慧

二重积分的基本形式常写为∫∫f(x,y)dxdy，这里的dxdy不仅仅是一个符号，它蕴含着积分计算的精髓——分步进行。想象一下，你站在一片被划分为无数小矩形的田野上，每个小矩形的“重量”或“价值”由它所在位置的函数值f(x,y)决定。要计算整片田野的总“重量”，你可以先沿着一个方向（比如x轴）将所有小矩形的“重量”累加起来，得到一系列“线”上的累积值；然后，再沿着另一个方向（y轴）将这些“线”上的累积值进一步累加，最终得到整个区域的累积总和。

三、实战演练：一步步求解二重积分

第一步：明确积分区域

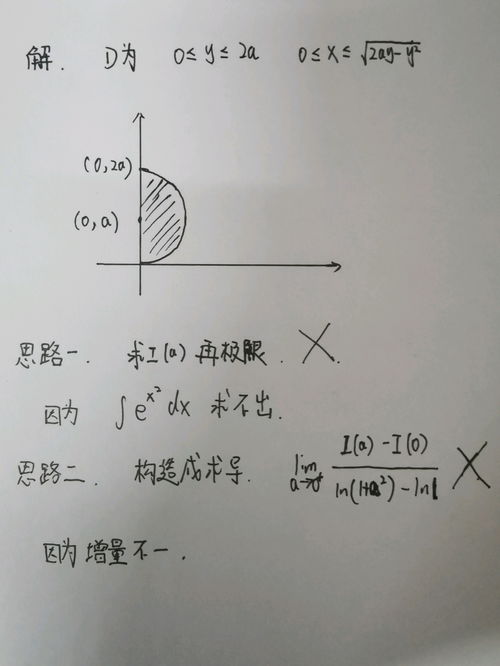
一切计算始于明确。首先，你需要知道要计算的是哪个区域内的二重积分。这个区域可以是矩形、圆形、椭圆形，甚至是更复杂的图形。明确积分区域后，你可以通过画图的方式直观地理解它，并尝试找出该区域在x轴和y轴上的投影范围，这将成为你设定积分上下限的重要依据。

第二步：选择合适的积分次序

二重积分的计算顺序并不是唯一的，你可以选择先对x积分再对y积分（即∫dy∫f(x,y)dx），也可以选择先对y积分再对x积分（即∫dx∫f(x,y)dy）。选择哪种顺序取决于积分区域的形状、被积函数的性质以及你的个人偏好。一般来说，如果积分区域在x轴上更容易描述，或者函数f(x,y)关于x更容易积分，那么先对x积分可能是个不错的选择。

第三步：确定积分上下限

一旦确定了积分次序，接下来就是确定每个积分变量的上下限。这通常需要根据积分区域的边界来设定。比如，如果先对x积分，那么x的积分下限和上限将是y的某个函数，表示在给定y值下，x的取值范围。

第四步：执行积分运算

有了积分次序和上下限，接下来就可以进行实际的积分运算了。注意，这一步可能涉及到基本的积分技巧、换元积分、分部积分等高等数学知识。不过，不要害怕，因为每一步都是基于前面步骤的合理推理和设定。

第五步：检查结果

完成积分后，别忘了检查结果的合理性。有时候，通过不同的积分次序会得到相同的结果，这可以作为验证你计算过程是否正确的一个手段。此外，你也可以利用一些物理或几何意义来辅助理解你的答案是否合理。

四、二重积分的魅力所在：理论与应用的完美结合

二重积分之所以如此迷人，不仅仅在于它复杂的计算过程，更在于它广泛的应用领域。从物理学中的质量分布、电荷分布，到工程学中的压力计算、流体动力学，再到经济学中的成本估算、收益分析，二重积分无处不在。它如同一把万能钥匙，为我们打开了一个又一个未知世界的大门。

结语

通过这场关于“二重积分dxdy怎么算”的旅程，我们不难发现，二重积分不仅是一个数学工具，更是一种思维方式。它教会我们如何将复杂的问题分解成简单的部分，通过逐步推理和计算来找到答案。在这个过程中，我们既锻炼了逻辑思维和抽象能力，又感受到了数学与现实的紧密联系。因此，无论你是数学爱好者还是专业人士，掌握二重积分都将是你探索未知世界、解决实际问题的有力武器。