揭秘二进制与十进制：数字世界的互换魔法

在计算机科学和数字电子领域，二进制数与十进制数之间的相互转换是基础且至关重要的知识。这两种数制不仅在计算机内部表示数据和执行运算时发挥着核心作用，也是理解计算机底层工作原理的关键。本文将从基本概念出发，深入探讨二进制数与十进制数之间的转换方法，以及这些转换在实际应用中的重要性。

首先，我们需要明确二进制数和十进制数的基本概念。二进制数，或称二进位计数制，是一种数学上的数制，它只有两个基本符号：0和1。这种数制在计算机内部被广泛采用，因为计算机中的所有信息，无论是文本、图像还是声音，最终都被转换成二进制代码进行存储和处理。相比之下，十进制数是我们日常生活中最常用的数制，它基于十个基本符号：0到9。十进制数的每一位（或称数位）的权重是10的幂次方，从右至左依次为10^0、10^1、10^2，以此类推。

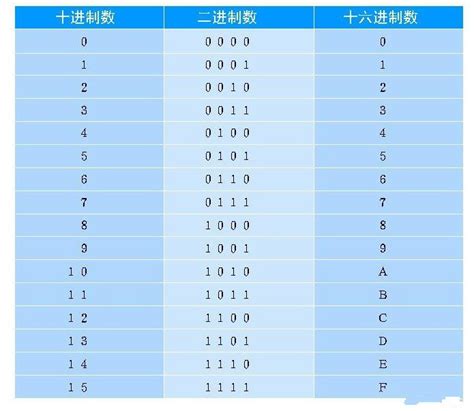
接下来，我们探讨如何将二进制数转换为十进制数。这个过程相对简单直接，只需将二进制数中的每一位与其对应的权重相乘，然后将所有乘积相加即可。例如，二进制数1011转换为十进制数的步骤如下：从右至左，最右边的位（或称最低位）的权重为2^0（即1），然后依次向左，权重分别为2^1（即2）、2^2（即4）、2^3（即8）。因此，二进制数1011中的每一位分别对应的十进制数为1×1（即1）、0×2（即0）、1×4（即4）、1×8（即8）。将这些乘积相加，得到1+0+4+8=13。所以，二进制数1011等于十进制数13。

反过来，将十进制数转换为二进制数则稍显复杂，但同样遵循一定的规则。这个过程通常通过“除2取余法”来实现。具体步骤如下：首先，将十进制数除以2，记下余数；然后，将得到的商再次除以2，并记下新的余数；重复这个过程，直到商为0为止。最后，将所有记下的余数从下到上依次排列，即可得到对应的二进制数。例如，将十进制数13转换为二进制数的过程如下：13除以2得到商6余1，6除以2得到商3余0，3除以2得到商1余1，1除以2得到商0余1。因此，将余数从下到上排列得到1101，即十进制数13对应的二进制数。

值得注意的是，二进制数与十进制数之间的转换不仅限于上述的直接转换方法。在实际应用中，特别是在处理大量数据时，我们可能需要更高效、更快速的转换算法。例如，利用位运算可以加速二进制数的处理；而使用查找表（或称映射表）则可以快速实现十进制数到二进制数的转换，尤其是在固定位数的情况下。这些高级技巧和方法虽然超出了基础知识的范畴，但对于深入理解计算机科学和提高编程效率具有重要意义。

此外，二进制数与十进制数之间的转换在计算机科学中的应用广泛而深远。在数据通信领域，二进制数的简洁性和稳定性使其成为数据传输的理想选择。无论是通过网络传输的文件、图像还是视频，它们最终都被转换成二进制代码进行传输。这种转换不仅提高了数据的传输效率，还降低了数据在传输过程中出错的可能性。在数据存储方面，二进制数的紧凑性使得它能够以更小的空间存储更多的信息。这对于现代计算机系统中的海量数据存储需求至关重要。

在编程和软件开发中，二进制数与十进制数之间的转换也是不可或缺的一部分。程序员经常需要在代码中处理不同数制之间的转换，以确保数据的正确性和程序的稳定性。例如，在处理图像和音频文件时，程序员可能需要将这些文件从二进制格式转换为十进制格式进行进一步处理；在编写加密算法时，二进制数的运算和转换也是实现安全通信的关键。

除了计算机科学领域外，二进制数与十进制数之间的转换在其他学科和领域中也具有广泛的应用。在电子工程中，二进制数被广泛应用于数字电路和数字系统的设计。在数字信号处理领域，二进制数的转换和处理是实现信号分析和处理的基础。在生物医学工程中，二进制数的应用也日益广泛，例如在基因测序和生物信息学研究中发挥着重要作用。

总之，二进制数与十进制数之间的相互转换是计算机科学和数字电子领域的基础知识之一。它不仅对于理解计算机底层工作原理至关重要，还在数据通信、数据存储、编程和软件开发等多个方面发挥着重要作用。通过深入学习和掌握这些转换方法和技巧，我们可以更好地利用计算机技术的优势来解决实际问题，推动科技和社会的快速发展。随着计算机科学和技术的不断进步和创新，我们有理由相信，二进制数与十进制数之间的转换将在未来继续发挥重要作用，为人类社会带来更多的便利和进步。