二进制转换为十进制
在现代计算机科学的基石中,二进制与十进制是两种最为基础且重要的数制。对于大多数非计算机专业人士而言,十进制是日常生活中最常用的数制,从数数、计算到货币交易,无不体现出十进制的身影。而二进制,则像是计算机世界的“秘密语言”,是计算机内部数据处理和存储的基础。本文将深入探讨二进制转十进制的过程,帮助读者从理论到实践,全面理解这一转换。

一、二进制与十进制的基本概念
首先,我们需要明确二进制和十进制的基本概念。

十进制:这是我们日常使用的数制,也称为阿拉伯数字系统,它基于10个基本符号:0, 1, 2, 3, 4, 5, 6, 7, 8, 9。每一位的权重是10的幂次方,从右至左分别为10^0(个位)、10^1(十位)、10^2(百位)等。

二进制:二进制数制只包含两个基本符号:0和1。每一位的权重是2的幂次方,从右至左分别为2^0(个位)、2^1(二位)、2^2(四位)等。二进制是计算机内部信息处理的基础,因为计算机中的所有信息,包括文字、图像、声音等,最终都被转化为二进制代码进行存储和运算。
二、二进制转十进制的方法
二进制转十进制的过程,就是将二进制数中每一位上的数字乘以对应的权重(2的幂次方),然后将这些乘积相加。这个过程类似于我们在十进制下做乘法累加的操作。
步骤:
1. 确定二进制数的位数:首先,我们需要知道二进制数的长度,即它有多少位。例如,二进制数1011有4位。
2. 从右至左,计算每一位的权重:从二进制数的最右边开始,每一位的权重是2的幂次方,幂次从0开始递增。例如,对于二进制数1011,从右至左的权重分别是2^0(1)、2^1(2)、2^2(4)、2^3(8)。
3. 将每一位上的数字与对应的权重相乘:接下来,我们将二进制数中每一位上的数字(0或1)与对应的权重相乘。例如,对于二进制数1011,计算过程如下:
最右边一位是1,权重是2^0=1,所以乘积是1*1=1;
第二位是0,权重是2^1=2,所以乘积是0*2=0;
第三位是1,权重是2^2=4,所以乘积是1*4=4;
最左边一位是1,权重是2^3=8,所以乘积是1*8=8。
4. 将所有乘积相加:最后,我们将所有乘积相加,得到的结果就是二进制数对应的十进制数。对于二进制数1011,计算过程如下:
1(最右边一位的乘积)+ 0(第二位的乘积)+ 4(第三位的乘积)+ 8(最左边一位的乘积)= 13
因此,二进制数1011转换为十进制数是13。
三、二进制转十进制的实例分析
为了更好地理解二进制转十进制的过程,我们可以分析几个具体的例子。
例子1:二进制数1101
权重:2^0=1, 2^1=2, 2^2=4, 2^3=8
每一位上的数字与权重的乘积:1*1=1, 1*2=2, 0*4=0, 1*8=8
所有乘积相加:1+2+0+8=11
因此,二进制数1101转换为十进制数是11。
例子2:二进制数10000
权重:2^0=1, 2^1=2, 2^2=4, 2^3=8, 2^4=16
每一位上的数字与权重的乘积:0*1=0, 0*2=0, 0*4=0, 0*8=0, 1*16=16
所有乘积相加:0+0+0+0+16=16
因此,二进制数10000转换为十进制数是16。
例子3:二进制数11111
权重:2^0=1, 2^1=2, 2^2=4, 2^3=8, 2^4=16
- 上一篇: 揭秘:德玛西亚背后的传奇故事
- 下一篇: 微信账单轻松查,支出明细一目了然
-
 二进制转换为十进制的方法资讯攻略11-10
二进制转换为十进制的方法资讯攻略11-10 -
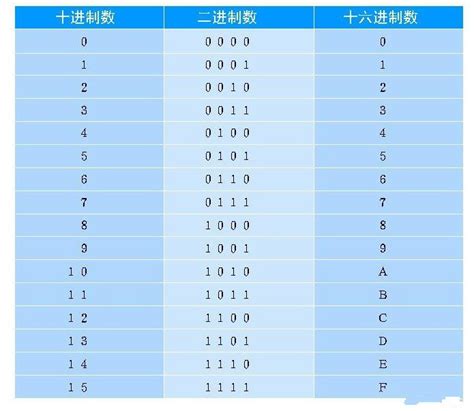 揭秘:十进制数变身二进制数的神奇转换法资讯攻略12-08
揭秘:十进制数变身二进制数的神奇转换法资讯攻略12-08 -
 二进制如何转换成十进制?资讯攻略11-11
二进制如何转换成十进制?资讯攻略11-11 -
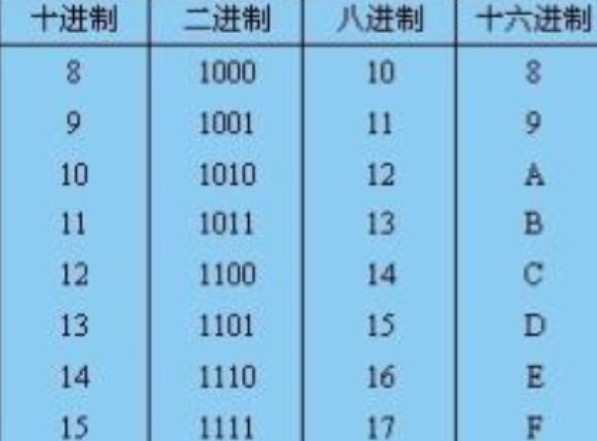 十六进制转换方法资讯攻略11-26
十六进制转换方法资讯攻略11-26 -
 十六进制转二进制的详细方法资讯攻略11-07
十六进制转二进制的详细方法资讯攻略11-07 -
 揭秘!一键学会十进制到二进制的神奇转换法资讯攻略10-27
揭秘!一键学会十进制到二进制的神奇转换法资讯攻略10-27












