揭秘!一键学会十进制到二进制的神奇转换法
在日常生活中,我们习惯了使用十进制数(0-9)来计数和做计算,但在计算机的世界里,一切都被简化为二进制(0和1)的语言。这种转换不仅是计算机科学的基础,也是现代科技得以快速发展的基石。下面,我们就来一步步探索如何从我们熟悉的十进制转换到神秘的二进制,让这个过程变得既简单又有趣。

为什么要转换到二进制?
首先,了解一下为什么计算机要使用二进制而非十进制。主要原因有几点:

1. 简化电路设计:二进制只有两个状态(0和1),可以直接用电子元件的开关状态来表示,极大地简化了电路的设计和实现。

2. 提高运算速度:二进制运算规则简单,执行速度快,非常适合快速计算。
3. 减少错误:只有两个状态的系统相比多状态系统,在传输和存储数据时出错的可能性更低。
十进制转二进制的原理
十进制数转换为二进制数,实际上是将十进制数不断地除以2,记录下每次除法的余数,然后将这些余数逆序排列。这里的“逆序”很关键,因为它决定了最终二进制数的正确性。
详细步骤
第一步:理解基础
想象你手里有一些糖果,要和朋友平均分配,但只能分成两半(不考虑切不均匀的情况)。每次分配后,你都会记录下自己手里的糖果数量(即余数),然后继续用剩下的糖果进行下一次分配,直到没有糖果可以再分(即商为0)。这个过程其实就是在做十进制到二进制的转换,只不过我们的“糖果”是十进制数,而“分成两半”就是除以2。
第二步:动手实践
假设我们要将十进制数`23`转换为二进制数。
1. 首次除2:将23除以2,得到商11和余数1。这里,余数1是二进制数最右边的数。
$$ 23 \div 2 = 11 \text{ 余 } 1 $$
2. 继续除2:用上一步的商11再除以2,得到商5和余数1。新得到的余数1添加到之前记录的余数1的左边。
$$ 11 \div 2 = 5 \text{ 余 } 1 $$
3. 重复步骤:继续用商5除以2,得到商2和余数1。继续记录余数。
$$ 5 \div 2 = 2 \text{ 余 } 1 $$
4. 直到商为0:用商2除以2,得到商1和余数0。虽然0在二进制中也很重要,但它通常不被省略(特别是在初学者理解阶段)。
$$ 2 \div 2 = 1 \text{ 余 } 0 $$
5. 最后一步:用商1再除以2,得到商0和余数1。当商为0时,表示所有的十进制数都已转换成二进制数。
$$ 1 \div 2 = 0 \text{ 余 } 1 $$
6. 逆序排列:将所有记录的余数从下到上(即按照计算顺序)排列,得到最终的二进制数`10111`。
技巧与注意事项
逆序排列:非常重要的一步,确保最后得到的二进制数是正确的。
理解余数:每次除法的余数就是二进制数中的一位,从最右边开始记录。
直到商为0:只有当商变为0时,才意味着所有的十进制数都已转换成二进制数。
简化操作:在实际操作中,可以直接通过手写或使用计算器来完成这些除法,但理解背后的原理更为重要。
进阶理解
为了进一步加深理解,我们可以考虑十进制小数转换为二进制小数的方法,虽然这通常涉及更复杂的循环或逼近过程,但基本原理相似——不断乘以2并观察整数部分(对于小数部分而言)。
结语
从十进制到二进制的转换,看似复杂,实则遵循着简单的数学规则。通过不断实践和理解背后的原理,我们可以轻松掌握这一技能。在计算机的底层世界里,二进制不仅仅是数字和符号的堆砌,它是连接现实世界与数字世界的桥梁,是科技进步的基石。希望这篇文章能让你对十进制到二进制的转换有一个清晰而深刻的认识,从而开启你探索计算机世界的奇妙之旅。
-
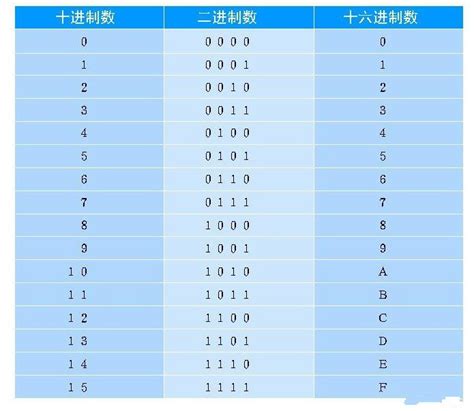 揭秘:十进制数变身二进制数的神奇转换法资讯攻略12-08
揭秘:十进制数变身二进制数的神奇转换法资讯攻略12-08 -
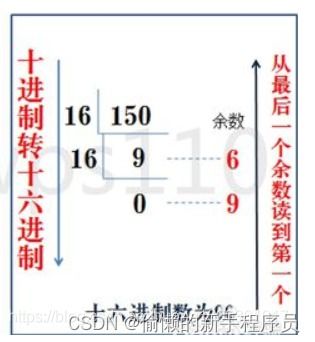 轻松学会:16进制转10进制的方法资讯攻略11-23
轻松学会:16进制转10进制的方法资讯攻略11-23 -
 二进制转换为十进制资讯攻略11-10
二进制转换为十进制资讯攻略11-10 -
 十六进制转二进制的详细方法资讯攻略11-07
十六进制转二进制的详细方法资讯攻略11-07 -
 二进制转十进制的方法资讯攻略11-10
二进制转十进制的方法资讯攻略11-10 -
 揭秘二进制与十进制:数字世界的互换魔法资讯攻略12-06
揭秘二进制与十进制:数字世界的互换魔法资讯攻略12-06












