揭秘:十进制数变身二进制数的神奇转换法
十进制如何转换为二进制
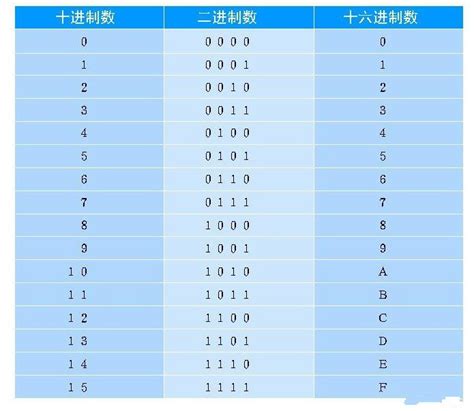
十进制数是我们日常生活中最常用的数制,每一位上的数码都是0\~9之间的数字。而二进制数在计算机内部被广泛使用,它的每一位数码只能是0或1。将十进制数转换为二进制数,是理解计算机如何处理和存储数据的基础。本文将详细介绍几种常用的十进制到二进制的转换方法,帮助读者轻松掌握这一技能。
方法一:除2取余法
除2取余法是最直观、最常用的十进制转二进制的方法。具体步骤如下:
1. 将十进制数除以2:记录余数(只可能是0或1),并将商继续除以2。
2. 重复上述步骤:直到商为0为止。
3. 将得到的余数从下到上排列:这些余数就是二进制数的各位。
示例
将十进制数23转换为二进制数:
1. 23 ÷ 2 = 11 余 1
2. 11 ÷ 2 = 5 余 1
3. 5 ÷ 2 = 2 余 1
4. 2 ÷ 2 = 1 余 0
5. 1 ÷ 2 = 0 余 1
将余数从下到上排列,得到二进制数:10111。
方法二:乘2取整法
乘2取整法是通过不断将十进制数乘以2,并取结果的整数部分,直到结果为1或0时停止,然后将每一步的整数部分从高位到低位排列,得到二进制数。不过需要注意的是,这种方法在实际操作中不如除2取余法直观和常用,更多用于理解二进制与十进制之间的转换关系。
示例
将十进制数23转换为二进制数:
1. 23 × 2 = 46(整数部分为46,小数部分为0,记录整数部分46)
2. 因为46不是1或0,继续:46 × 2 = 92(整数部分为92,小数部分为0,记录整数部分92)
(注意:这一步实际上不会直接用在转换过程中,因为我们会发现直接对23进行连续乘2并取整的方法不如除2取余法直接。但为了展示乘2取整法的步骤,这里暂时保留。)
然而,为了简化说明,我们实际上会直接从23开始,通过不断除以2的反向思考来理解:
如果我们从23开始,想象它已经是一个二进制数的十进制表示,那么要找到比这个数小的最大的2的幂次,这里是2^4=16(但这一步不是直接用在转换中的,只是为了说明思路)。
然后我们会想,23减去16(即2^4的下一个幂次之前的所有值之和,或者说是在二进制表示中对应位为1的最大值),剩下7,这表示23的二进制表示中,从高位到低位数的第四位是1(因为2^4>23>2^3)。
接着对7重复这个过程,找到比7小的最大的2的幂次是2^2=4,7-4=3,表示二进制数的第三位是1。
再对3重复,找到2^1=2,3-2=1,表示二进制数的第二位是1。
最后对1,2^0=1,1-1=0,表示二进制数的最低位(第一位)是1。
但直接这样解释可能仍然有些抽象,实际上我们回到乘2取整法的直观理解上,更常见的做法还是直接采用除2取余法。不过,为了说明乘2取整法的逻辑完整性,我们可以这样理解其背后的原理:不断乘2相当于在十进制数后面补0(即乘以10的二进制等价操作,但因为二进制中只有0和1,所以实际上是每次乘以基数2),然后通过取整(即去掉小数部分,只保留整数部分)来逼近原始的十进制数在二进制下的表示。但这种方法在实际操作时不如除2取余法方便和直接。
因此,虽然乘2取整法在理论上可以解释十进制到二进制的转换过程,但在实际应用中,我们更推荐使用除2取余法。
方法三:快速转换法(适用于已知二进制位数的十进制数)
对于某些已知二进制位数的十进制数,我们可以采用快速转换法。这种方法通常用于需要快速判断一个十进制数在特定位数下的二进制表示时。具体方法是:将十进制数对应的二进制位数的每一位看作是一个二进制位(从右到左分别为0位、1位、2位...),然后计算十进制数中每一位数字在二进制表示中的贡献。这种方法需要一定的二进制和十进制之间的转换经验,以及对二进制位权的理解。
示例(简化说明)
- 上一篇: 轻松学会!折纸飞镖制作教程
- 下一篇: 揭秘!阿拉伯数字1到10的大写奥秘,你知道吗?
-
 揭秘!一键学会十进制到二进制的神奇转换法资讯攻略10-27
揭秘!一键学会十进制到二进制的神奇转换法资讯攻略10-27 -
 揭秘二进制与十进制:数字世界的互换魔法资讯攻略12-06
揭秘二进制与十进制:数字世界的互换魔法资讯攻略12-06 -
 十六进制转换方法资讯攻略11-26
十六进制转换方法资讯攻略11-26 -
 BCD码如何轻松换算资讯攻略11-06
BCD码如何轻松换算资讯攻略11-06 -
 二进制如何转换成十进制?资讯攻略11-11
二进制如何转换成十进制?资讯攻略11-11 -
 二进制转换为十进制资讯攻略11-10
二进制转换为十进制资讯攻略11-10












