双曲线准线绘制教程

双曲线的准线，作为双曲线的一个重要几何特征，是数学研究和教学中不可或缺的一部分。对于那些对双曲线的准线画法感兴趣的读者来说，本文将详细介绍双曲线的准线定义、性质及具体画法，旨在帮助大家深入理解并掌握这一知识点。

首先，我们需要明确双曲线的准线是什么。在数学中，双曲线是一种特殊的平面曲线，它由所有满足到两个定点（焦点）的距离之差为常数（且这个常数小于两焦点之间的距离）的点组成。而双曲线的准线，则是一条特殊的定直线，它与双曲线的焦点有着特殊的关系：平面内一个动点到一个定点（双曲线的焦点）与准线的距离之比是一个大于1的常数，这个常数即双曲线的离心率。

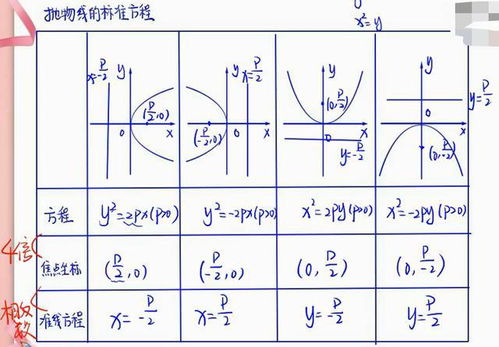
了解了双曲线的准线定义后，我们来看看它的性质。双曲线的准线有以下几个重要特点：

1. 双曲线有两条准线，分别位于双曲线的两侧，且关于双曲线的对称轴对称。

2. 当双曲线的焦点在x轴上时，其准线的方程为x=±a²/c，其中a是双曲线的实半轴长，c是双曲线的半焦距。类似地，当焦点在y轴上时，准线的方程则为y=±a²/c。

3. 准线与焦点的距离是一个固定的值，它等于c乘以（1+e），其中e是双曲线的离心率。

接下来，我们详细介绍双曲线的准线画法。根据不同的需求和情境，双曲线的准线可以通过多种方法绘制。以下是几种常见的画法：

方法一：利用双曲线的标准方程

如果双曲线的标准方程已知（如x²/a²-y²/b²=1），我们可以直接根据方程中的a和c值来计算准线的方程。然后，在坐标系中画出这条直线。具体步骤如下：

1. 根据双曲线的标准方程，确定a和b的值（注意：c的值可以通过c²=a²+b²计算得出）。

2. 将a和c的值代入准线的方程x=±a²/c（焦点在x轴上）或y=±a²/c（焦点在y轴上）。

3. 在坐标系中画出这条直线，即得到双曲线的一条准线。由于双曲线有两条准线，且关于对称轴对称，因此还需画出另一条准线。

方法二：利用双曲线的焦点和离心率

如果双曲线的焦点和离心率已知，我们也可以通过它们来计算准线的方程并画出准线。具体步骤如下：

1. 根据已知条件确定焦点F1和F2的坐标以及离心率e。

2. 利用公式c=e×a（其中c是半焦距，a是实半轴长）求出a的值（注意：这里需要假设一个a的初始值，然后通过迭代或其他方法使c的值满足已知条件）。

3. 将a和c的值代入准线的方程x=±a²/c（焦点在x轴上）或y=±a²/c（焦点在y轴上）。

4. 在坐标系中画出这条直线，即得到双曲线的一条准线。同样地，还需画出另一条准线。

方法三：利用几何作图法

除了上述两种方法外，我们还可以通过几何作图法来画出双曲线的准线。这种方法虽然不如前两种方法精确，但更直观、易于理解。具体步骤如下：

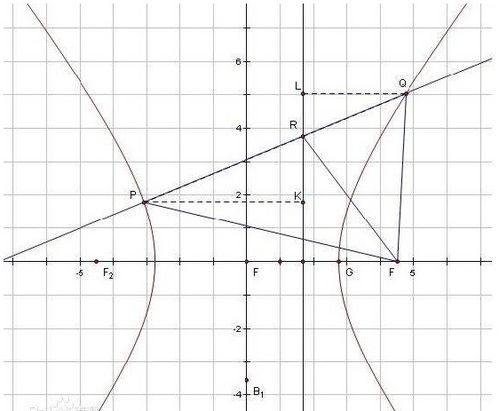
1. 在坐标系中画出双曲线的两个焦点F1和F2。

2. 选择双曲线上的一点P（注意：点P的选择是任意的，但为了便于观察和理解，建议选择离焦点较近的点）。

3. 分别连接PF1和PF2，并测量它们的长度。

4. 在PF2的延长线上取一点Q，使得|PF2|-|PF1|=|PQ|（这里的|PQ|应为一个小于|F1F2|的常数）。

5. 过点Q作一条垂直于PF2的直线l，即得到双曲线的一条准线（注意：这里的直线l是近似的准线，因为点P是任意选择的）。为了得到更精确的准线，可以重复上述步骤并选择多个点P进行平均或拟合。

6. 同样地，可以过点P在PF1的延长线上取一点R，并作出另一条近似的准线。

需要注意的是，几何作图法得到的准线通常是近似的，因为它依赖于点P的选择和测量的准确性。因此，在实际应用中，我们更倾向于使用前两种方法。

在掌握了双曲线的准线画法后，我们还可以进一步探索它与双曲线其他几何特征之间的关系。例如，准线与焦点的距离、准线与双曲线的对称轴之间的关系等。这些关系不仅有助于我们更深入地理解双曲线的性质，还能为我们在解决相关数学问题时提供有用的线索和思路。

此外，值得注意的是，虽然本文重点介绍了双曲线的准线