全面解锁!24个必备二重积分公式汇总
二重积分公式大全深度解析

在微积分领域中,二重积分是一个非常重要的工具,用于计算平面区域内某函数图形的面积、体积以及其他相关物理量。二重积分不仅在数学理论中占据重要地位,在工程、物理、经济等多个领域也有广泛的应用。为了帮助大家更全面地了解二重积分,本文精选了24个重要的二重积分公式,并进行详细解析。
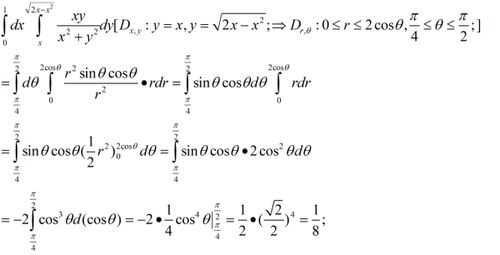
一、基本概念与性质

二重积分的基本形式是∫∫D f(x,y) dxdy,其中D是平面上的一个区域,f(x,y)是被积函数。计算二重积分时,通常需要选择适当的坐标系(直角坐标或极坐标)和积分次序(先对x后对y,或先对y后对x)。

性质1(线性性质):对于任意常数a、b和函数u(x,y)、v(x,y),有∫∫D [au(x,y)+bv(x,y)] dxdy = a∫∫D u(x,y) dxdy + b∫∫D v(x,y) dxdy。
性质2(积分区域的可加性):若区域D可划分为两个互不重叠的子区域D1和D2,则∫∫D f(x,y) dxdy = ∫∫D1 f(x,y) dxdy + ∫∫D2 f(x,y) dxdy。
性质3(积分中值定理):存在某个点(x0,y0)∈D,使得∫∫D f(x,y) dxdy = f(x0,y0) * S(D),其中S(D)是区域D的面积。
二、直角坐标系下的二重积分
1. 矩形区域上的二重积分:若D=[a,b]×[c,d],则∫∫D f(x,y) dxdy = ∫a→b [∫c→d f(x,y) dy] dx = ∫c→d [∫a→b f(x,y) dx] dy。
2. 改变积分次序:通过绘制积分区域的图形,确定新的积分上下限,从而改变积分次序。例如,将∫0→1 [∫y→1 (x+y) dx] dy变为∫0→1 [∫0→x (x+y) dy] dx。
3. 分段函数在矩形区域上的二重积分:将区域D划分为若干子区域,分别计算各子区域上的二重积分,然后求和。
4. 利用对称性简化计算:若函数f(x,y)关于某条直线或某个点对称,可利用对称性简化二重积分的计算。
5. 极值定理的应用:若f(x,y)在D上连续,且存在最大值M和最小值m,则m*S(D) ≤ ∫∫D f(x,y) dxdy ≤ M*S(D)。
三、极坐标系下的二重积分
1. 极坐标与直角坐标的转换:x=r*cosθ,y=r*sinθ,dxdy=r dr dθ。
2. 极坐标系下的二重积分形式:若D是由θ=α、θ=β、r=ρ1(θ)、r=ρ2(θ)所围成的区域,则∫∫D f(x,y) dxdy = ∫α→β [∫ρ1(θ)→ρ2(θ) f(r*cosθ,r*sinθ) r dr] dθ。
3. 圆形区域上的二重积分:若D为圆心在原点半径为R的圆,则∫∫D f(x,y) dxdy = ∫0→2π [∫0→R f(r*cosθ,r*sinθ) r dr] dθ。
4. 环形区域上的二重积分:若D为内外半径分别为r1和r2的圆环,则∫∫D f(x,y) dxdy = ∫0→2π [∫r1→r2 f(r*cosθ,r*sinθ) r dr] dθ。
5. 扇形区域上的二重积分:若D为圆心在原点、半径为R、夹角为α的扇形,则∫∫D f(x,y) dxdy = ∫0→α [∫0→R f(r*cosθ,r*sinθ) r dr] dθ。
四、特殊函数的二重积分
1. 幂函数的二重积分:如∫∫D x^m y^n dxdy,可通过换元积分法或分部积分法求解。
2. 三角函数的二重积分:如∫∫D sin(x+y) dxdy,可利用三角函数的和差化积公式和对称性进行简化。
3. 指数函数的二重积分:如∫∫D e^(x+y) dxdy,可通过先对其中一个变量积分,再利用指数函数的性质求解。
4. 对数函数的二重积分:如∫∫D ln(x^2+y^2) dxdy,可通过极坐标转换和分部积分法求解。
5. 分段函数的二重积分:如f(x,y)={x+y, x≥y; x-y, x
五、二重积分的物理应用
1. 面积计算:当f(x,y)=1时,∫∫D dxdy即为区域D的面积。
2. 体积计算:如计算由曲面z=f(x,y)与平面z=0、x=a、x=b、y=c、y=d所围成的体积,可转化为二重积分∫∫D f(x,y) dxdy。
3. 质心计算:对于均匀分布的平面图形,其质心坐标可通过二重积分求解。
4. 转动惯量计算:对于绕某轴旋转的平面图形,其转动惯量可通过二重积分计算。
5. 引力势能与电场强度计算:在物理学中,二重积分可用于计算引力势能和电场强度等物理量。
六、计算技巧与注意事项
1. 选择合适的坐标系:根据被积函数和积分区域的特点,选择合适的坐标系(直角坐标或极坐标)进行计算。
2. 确定积分次序:通过绘制积分区域的图形,确定积分次序和积分上下限。
3. 利用对称性简化计算:若函数或积分区域具有对称性,可利用对称性简化计算过程。
4. 分步计算与合并:对于复杂的被积函数或积分区域,可将其分解为若干简单部分分别计算后合并结果。
5. 注意积分限的变化:在改变积分次序或进行坐标转换时,要注意积分限的变化情况。
通过以上对二重积分公式的详细解析和分类归纳,相信读者对二重积分有了更深入的理解和掌握。在实际应用中,应根据具体问题选择合适的公式和方法进行计算,并注意计算过程中的细节和技巧。
- 上一篇: 家常美味秘籍:轻松学会做粉丝汤
- 下一篇: 解锁高德地图:一键查看全部历史足迹的秘密
-
 解锁数据奥秘:全面汇总资料分析必备公式资讯攻略11-01
解锁数据奥秘:全面汇总资料分析必备公式资讯攻略11-01 -
 揭秘二重积分的计算方法,并通过例题轻松掌握!资讯攻略01-18
揭秘二重积分的计算方法,并通过例题轻松掌握!资讯攻略01-18 -
 轻松掌握二重积分dxdy的计算方法资讯攻略10-24
轻松掌握二重积分dxdy的计算方法资讯攻略10-24 -
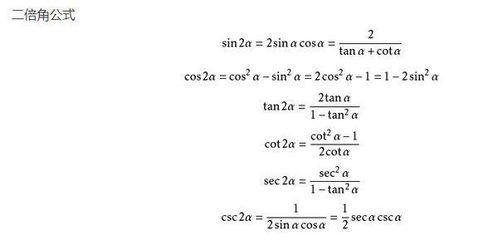 精通常见三角函数积分:公式推导与全面总结资讯攻略11-18
精通常见三角函数积分:公式推导与全面总结资讯攻略11-18 -
 全面解锁!《崩坏星穹铁道》椒丘角色养成必备材料大搜集,打造顶尖战力之路资讯攻略10-20
全面解锁!《崩坏星穹铁道》椒丘角色养成必备材料大搜集,打造顶尖战力之路资讯攻略10-20 -
 崩坏星穹铁道:貊泽角色养成必备材料全面汇总资讯攻略10-18
崩坏星穹铁道:貊泽角色养成必备材料全面汇总资讯攻略10-18